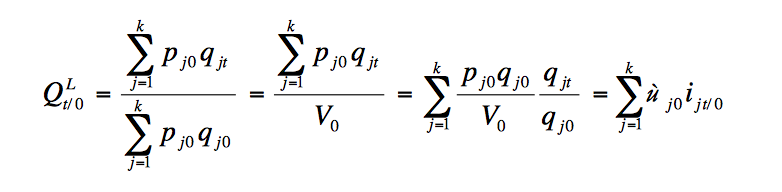Un índice de volumen encadenado se obtiene mediante la acumulación de datos y el producto sucesivo de los mismo. Son como «eslabones» que se van añadiendo poco a poco a la cadena para obtener un índice mucho más fiable y consistente. Es decir obtendríamos una serie temporal, que nos permitiría saber con mucha más exactitud los cambios que se han podido dar en una variable a lo largo del tiempo.
La utilización de este nuevo método sustituye a las mediciones que se hacían con datos o precios corrientes y base fija. Pero no todo son ventajas, pues esta nueva forma de medición tiene una importante pérdida de agregados. Para que nos entendamos, la suma de cada factor o dato mediante índices encadenados, no coincidirá con la suma obtenida por otro método. También es más costoso a la hora de realizar los cálculos, así como la explicación del resultado final.
Metodología
En primer lugar debemos tener en cuenta lo que es un número índice. Muchas veces, resulta difícil estudiar una evolución, por la dificultad de sus variables, por lo que para hacer estos datos más sencillos, se utilizan números índice, con un año base, y en función de este la variación de los demás años. Pudiendo utilizar como año base cualquiera de ellos.
Además, se pueden incluir varias variables, y sobre todo una medida que retiene las características dinámicas de las series originales. Esta nueva metodología se compone principalmente de un índice elemental que refleja las variaciones a lo largo del tiempo de un determinado factor. Lo explicaremos con un ejemplo.
Imaginemos que tenemos dos bienes A y B, con la producción y el precio de cada uno en varios años. Lo que haremos será crear un índice elemental para cada producto que mida la relación de la producción en un momento determinado con la producción de un año base. Con esto obtendremos un dato por cada bien y período, que compararemos con el año base. De este modo sabremos las posibles variaciones que ha tenido el bien respecto a un año.
A continuación, crearemos los índices encadenados. Relacionando la suma de ambos productos en un año determinado con la suma de ambos productos en el año base. Así obtendremos la evolución agregada de ambos bienes.
Es a este punto al que nos referíamos al explicar algunos de los inconvenientes de los índices encadenados. Pues la suma de los índices simples no dará igual que el resultado del índice compuesto. Es la pérdida de agregados.
En el caso de querer estudiar también las variaciones con precios y producción, tendremos que multiplicar cada cantidad producida por el precio correspondiente a ese año. Esto se hará en los índices simple y de nuevo se volverán a sumar.
Un índice de volumen encadenado es un indicador de la producción que valora la producción de cada año a los precios del año anterior. Esto supone una mejoría en relación a cómo se calculaba antes, ya que la base se modificaba cada diez años e iba pareciéndose cada vez menos a la realidad.
Con esta medición, se puede también aislar el efecto de algunos factores, manteniendo siempre su valor del año base. Es lo que llamamos Laspeyres. Un método utilizado para la elaboración de las principales estadísticas del INE. Es un índice aparentemente sencillo, pero al agregar todos los bienes o factores influyentes en la economía, el estudio resulta bastante más complicado.
La expresión de este índice es:
Las características de este índice son:
- La estructura de ponderaciones es fija y está fechada en el período base: m=0 en [3.1].
- La estructura del índice es una combinación lineal convexa de índices cuánticos elementales.
- Índice aditivo, al que se pueden añadir variables de forma sencilla y automática.
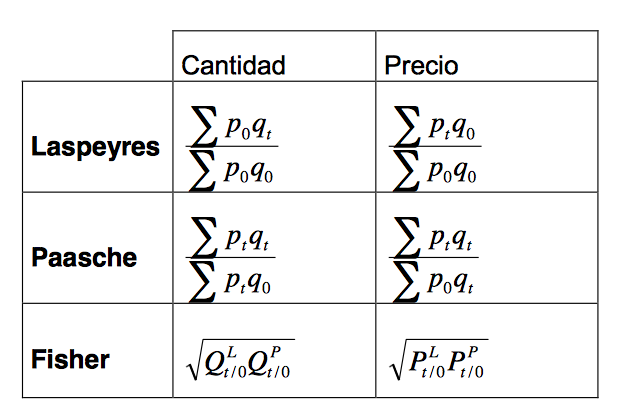
A continuación, tenemos una tabla resumen con las principales formulas que utilizan en el INE para calcular diferentes datos estadísticos.
Índice de Volumen Encadenados
En los índices compuesto se incluyen dos variables, t (período actual) y 0 (período base). Las diferencias entre dichos índices surgen en la forma de agregar los índices con ponderaciones del período base (Laspeyres) o del actual (Paasche).
Los índices encadenados consideran que el paso del período 0 al t se puede fragmentar, considerando incrementos parciales, esto es el encadenamiento de los índices.